
This look up is a fast operation because we eliminate half the nodes from our search on each iteration by choosing to follow the left subtree or the right subtree. This is particularly useful for data storage. One advantage of a binary search tree is that the lookup operation is fast and simple. It's based on the tree in the picture above. The following items are included in this Binary Search Tree example code. So, in general, (3) should be the answer. Note that (2) is for the bast case, and (4) is the answer for the worst case. That's because we need to know the structure of BST, and the height gives us that information (longest root-leaf path). What's the worst-case running time of search(or insert) operation in a binary search tree containing $n$ keys? We may appreciate the role of the height property of BST from the answer to the following question: Another thing to point out here is the importance of the height. The height (depth) could be anywhere from ~$log_2 n$(best case, perfectly balanced) to ~$n$ (worst case, a chain). So, the height of a tree is equal to the largest depth of any node in the tree. The height of a node in a tree is the number of edges (hops) on the longest downward path from the node to a leaf, and the height of a tree is the height of its root. A level of a tree consists of all nodes at the same depth. The length of the simple path from the root $r$ to a node $x$ is the depth of $x$ in $T$. The number of children of a node $x$ in a tree $T$ is the same as the degree of $x$. So, if extraction the max value needs to be fast, we should use a heap.Ī leaf (external) node is a node that has no children while nonleaf node is also called internal node. Consequently, the root node always has the largest value in the tree, which means that it's possible to find the maximum value in constant time: Simply return the root value. A heap is a tree in which each node's children have values less than or equal to node's value. The last tree out of major kinds of trees is a heap. The $ \log n$ behavior is the average case - it's possible for a particular tree to be much slower depending on its shape.
NAVIGATE A BINARY TREE TO DECODE MORSE CODE STRINGS CODE
Therefore, binary search trees are good for dictionary problems where the code inserts and looks up information indexed by some key. On average, a binary search tree algorithm can locate a node in an $n$ node tree in order $ \log n$ time (log base 2). The formal recursive definition is: a binary tree is either empty (represented by a null pointer), or is made of a single node, where the left and right pointers (recursive definition ahead) each point to a binary tree.Ī binary search tree (BST) or ordered binary tree is a type of binary tree where the nodes are arranged in order: for each node, all elements in its left subtree are less-or-equal to the node ().īasically, binary search trees are fast at insert and lookup. A null pointer represents a binary tree with no elements - the empty tree. The left and right pointers recursively point to smaller subtrees on either side. Of course you still have to write the decision to create the new node to the left or right side of this node.The root pointer points to the topmost node in the tree. The last valid pointer in the descending tree. Now you are making sure the loop stops while r is still a valid pointer. todo: code to bind a new node to r->right todo: code to bind a new node to r->leftĮlse // its always either '.' or '-' so there is no need to double check the symbol here You probably wants to extend your code to something more like this: for(int i = 0 i left)
The sooner you get to an element with two or more symbols in the morse code, your application crashes trying to read from r when it's a NULL pointer. You are not checking if r becomes NULL while looping. Howover, as there is only one element in the tree it will immediately become NULL for the next iteration when you set it to either r = r->left or r = r->right, as there is only one node in the tree and both it's left and right are NULL. When this loop starts, you make sure r is never NULL.
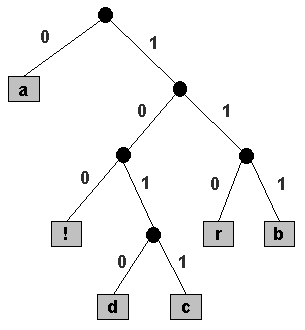
Your problem is here: for(int i = 0 i left The first 3 elements of my tree array get inserted but the program crashes when trying to insert "I". Void Insert(Node *&r, string letter, string code) I am trying to insert the Morse Code into a binary tree but my Insert() is acting up.


 0 kommentar(er)
0 kommentar(er)
